Description d'un fluide au repos

Dans cette leçon, nous allons décrire les fluides grâce à des grandeurs macroscopiques comme la pression p, la température etc, liées entre elles par la loi de la statique des fluides et la loi de Mariotte-Boyle. Ces grandeurs macroscopiques seront interprétées au niveau microscopique.

1. Qu’est-ce qu’un fluide ?

1. Description d’un fluide au repos.

Contrairement aux solides, les fluides n’ont pas de forme propre. Ce sont les liquides et les gaz.
Au niveau microscopique, les atomes ou les molécules peuvent glisser librement pour les liquides ou se déplacent librement pour les gaz.

Un fluide (liquide ou gaz) peut être décrit par des grandeurs macroscopiques comme la temprature T et la pression p.

• Au niveau microscopique, la température T (grandeur macroscopique) est liée à la vitesse des molécules ou agitation moléculaire ou agitation thermique.

• Au niveau microscopique, le pression p (grandeur macroscopique) est liée aux chocs des molécules sur les parois.

2. La pression et la force pressante.

La pression est définie à partir de la force pressante par la relation :

\[\boxed{ \huge p = \frac{F}{S} }\]

avec

p : pression en pascals (Pa)
F : force en newtons (N)
S : surface en mètres carrés (m²

Exemple d’application :

Le piston d’une pompe à vélo a une surface S =2,0 cm². Un sportif comprime l’air ans la pompe en appliquant une force de F = 100 N.
Quelle sera la pression p dans la pompe lorsque l’air sera comprimé ?

Réponse
Pression relative dans la pompe:
\[\Large p_r = \frac{F}{S} = \frac{50}{2,0\times10^{-4}} = 2,5 \times 10^5 \ Pa \]

Soit

\[\Large p_r = 2,5 \ bars \ (1 \ bar = 10^5 \ Pa) \]

Pression absolue dans la pompe (on ajoute la pression atmosphérique environ 1 bar) :

\[\Large p_a = 3,5 \ bars \]

3. La relation fondamentale de la statique des fuides.

Pour un fluide au repos, on peut exprimer la pression au point A d’altitude z_A en fonction de la pression au point B d’altitude z_B et de la masse volumique du fluide ρ.

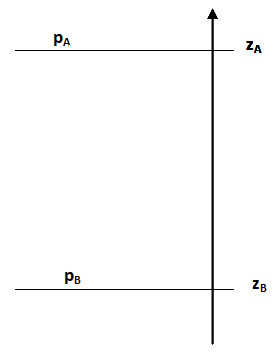
\[\boxed{ \huge p_B -p_A = \rho.g.(z_A - z_B) } \]

ou

\[ \boxed{\huge p_B + \rho.g.z_B = p_A + \rho.g.z_A } \]

Exemple d’application :

Un plongeur explore l’épave d’un bateau à 10 m de profondeur. A quelle pression (absolue) est soumis le plongeur ?
L’axe Oz sera orienté vers le haut et son origine sera prise à la surface.

Données :

\[
\large p_{atm} = 1,0 \ bar \newline
\large g = 9,8 \ N.kg^{-1} \newline
\large \rho_{eau} = 1,0.10^3 \ kg.m^{-3}
\]

Réponse :

Il est conseillé de faire un schéma du problème avec les axes et les valeurs des différentes grandeurs
Attention, avec l’orientation de l’axe prise, z_B est négatif (z_B = -10 m).

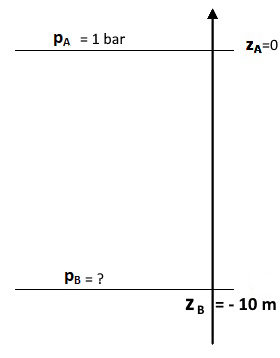
Appliquons la loi fondamentale de la statique des fluides au plongeur :
\[
\large p_B = \rho.g.(z_A - z_B) + p_A \newline
\large En \ prenant \ z_A = 0 \ ; \ z_B = -10 \ m \ et \ p_A = 1,0\times 10^5 \ Pa, \ il \ vient \ : \newline
\large p_B = 1,0.10^3 \times 9,81 \times (0 - (- 10 )) + 1,0.10^5 \newline
\large p_B = 1,98 . 10^5 \ Pa \approx 2,0.10^5 \ Pa \ (2 \ bar)
\]
On retrouve la règle des plongeurs : “la pression sous l’eau augmente d’environ 1 bar tous les 10 m”

4. La loi de Boyle - Mariotte.

Pour un gaz à une température T donnée et une quantité de matière n fixée, on a :

\[\boxed{ \huge p.V = constante }\]

Cette relation s’utilise ainsi :

\[\boxed{ \huge p_1.V_1 = p_2.V_2 }\]