Détermination d'une quantité de matière par titrage

• Un dosage permet de déterminer la quantité de matière ou la concentration d’une espèce chimique dissoute dans une solution.
• Un dosage par titrage ou titrage est une technique de dosage mettant en jeu une réaction chimique totale, rapide et unique.
• Lors d’un titrage colorimétrique, un changement de couleur du mélange réactionnel permet de repérer l’équivalence.

---

A l’équivalence du titrage, les réactifs ont été introduits 
dans les proportions stœchiométriques. 
Il y a changement de réactif limitant.

---

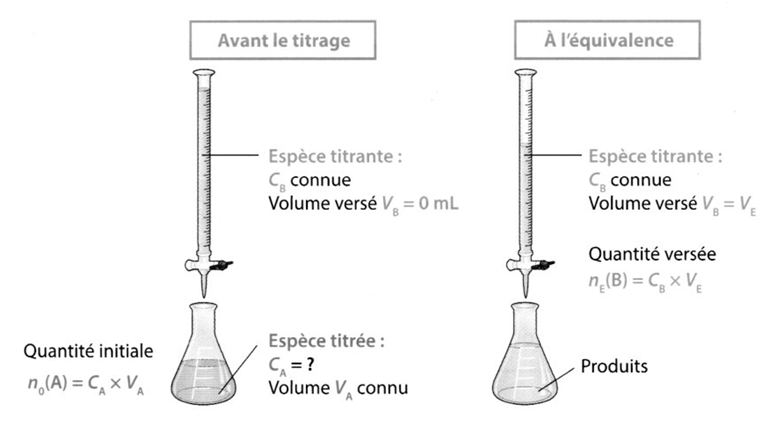
Pour la réaction suivante :

\[ aA + bB \rightarrow cC + dD\]

La relation entre les quantités de matière à l’équivalence est :

\[\frac{n(A)}{a} = \frac{n(B)}{b}\]
soit
\[\frac{C_A \times V_A}{a} = \frac{C_B \times V^E_B}{b}\]
On peut ainsi en déduire C_A

Application :

On dose un volume V₁ = 10 mL d’un produit phytosanitaire à base de fer II (Fe ²⁺ de concentration molaire C₁ inconnue, par une solution de permanganate de potassium (K⁺ + MnO₄^-) acidifié de concentration molaire C₂ = 0,030 mol.L^-1
Le volume de permanganate de potassium versé à l’équivalence vaut V_E = 9,6 mL.

1. Ecrire les demi-équations d’oxydoréduction des couples Fe³⁺ / Fe²⁺ et MnO₄^- / Mn²⁺
2. En déduire l’équation de la réaction du titrage.
3. Déterminer la relation entre les quantités de matière à l’équivalence.
4. Convertir cette relation avec les concentrations et les volumes.
5. Calculer la concentration C₁ en fer II de ce produit phytosanitaire.

Réponse
1.
\[ MnO_4^- + 8 H^+ + 5 e^- = Mn^{2+} + 4 H_2O \]
\[ + \;(Fe^{2+} = Fe^{3+} + e^-) \times 5 \]

---

\[ MnO_4^- + 8 H^+ + 5 Fe^{2+} = Mn^{2+} + 5Fe^{3+} + 4 H_2O \]
3. A l’équivalence, les réactifs on été introduits dans les proportions stoechiométriques, il y a changement de réactif limitant.
\[ \frac{n^E(MnO_4^-)}{1} = \frac{n(Fe^{2+})}{5} \]
4.
\[ C_2 \times V_2^E = \frac{C_1 \times V_1}{5} \]
5. Application numérique :
\[ C_1 = \frac{5 \times C_2 \times V_2^E}{V_1} \]

\[ C_1 = \frac{5 \times 0,030 \times 9,6 }{10} = 0,14 \; mol.L^{-1}\]