Interactions fondamentales et introduction à la notion de champ
Il existe 4 interactions fondamentales : forte, faible, électromagnétique et gravitationnelle.
Dans cet article, nous nous intéresserons à l’intéraction électrostatique (électromagnétique ou électrique) et à l’interaction gravitationnelle.
I- Notion de champ.
Les interactions sont modélisées par des vecteurs s’appliquant sur une masse pour l’interaction gravitationnelle et sur une charge pour l’interaction électrostatique.
Pour s’affranchir de la masse ou de la charge sur laquelle les forces s’appliquent, on a introduit la notion de champ.
Un champ vectoriel est une grandeur qui est ainsi définie en tout point de l’espace.
- Le champ gravitationnel est défini par :
\[ \Large \overrightarrow{G} = \frac{\overrightarrow{F_g}}{m}\]
- Le champ de pesanteur est défini par :
\[ \Large \overrightarrow{g} = \frac{\overrightarrow{P}}{m}\]
Par la suite, on assimilera le champ de pesanteur au champ gravitationnel, même s’il ne sont pas parfaitement identiques
\[ \Large \overrightarrow{F_g} \approx \overrightarrow{P} \; donc \; \overrightarrow{G} \approx \overrightarrow{g} \]
- Le champ électrostatique ou champ électrique est défini par :
\[ \Large \overrightarrow{E} = \frac{\overrightarrow{F_e}}{q}\]
II- L’interaction gravitationnelle.
L’interaction attractive entre deux masses mA et mB ponctuelles à la distantes de d s’écrit :
\[ \Large F_{A/B} = F_{B/A} = G.\frac{m_A.m_B}{d^2} \]
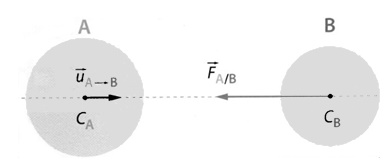
Pour le schéma ci-dessous, cette interaction de A sur B peut se modéliser par un vecteur force :
\[\Large \overrightarrow{F_{A/B}} = -G.\frac{m_A.m_B}{d^2}.\overrightarrow{u}_{A \rightarrow B}\]
Exemple :
- Donner l’expression littérale de la valeur de la force d’interacton gravitationnelle qui s’exerce sur un objet de masse m à la surface de la Terre.
- En déduire l’expression littérale de la valeur du champ de pesanteur assimilé au champ gravitationnel G = g
- En déduire la valeur du champ de pesanteur g.
Données :
Masse de la Terre : \[\Large M_T = 5,97 \times 10^{24} \; kg \]
Rayon de la Terre : \[\Large R_T = 6371 \; km \]
G : constante de gravitation universelle : \[\Large G = 6,67 \times 10^{–11} \; N.m^2.kg^{–2} \]
Réponse :
\[\Large \Large F_g = G.\frac{m.M_T}{R_T^2} \]
En assimilant la force d’interaction gravitationnelle au poids, on peut écrire :
\[ \Large F_g = G.\frac{m.M_T}{R_T^2} \approx P = m.g \]
soit
\[ \Large g = G.\frac{M_T}{R_T^2} \]Application numérique :
\[\Large g = 6,67.10^{-11}.\frac{5,97 \times 10^{24}}{(6,371 \times 10^6)^2} \]
\[\Large g \approx 9,8 \; N.kg^{-1} \]
III- L’interaction électrostatique
L’interaction attractive ou répulsive entre deux charges qA et qB ponctuelles à la distantes de d s’écrit :
\[ \Large F_{A/B} = F_{B/A} = k.\frac{|q_A.q_B|}{d^2} \]
avec \[\Large k = \frac{1}{4.\pi.\epsilon_0} = 9.10^9 N.m^2.C^{-2} \]
Cette relation s’appelle la loi de Coulomb et n’est valable que pour des charges ponctuelles.
L’expression vectorielle de l’interaction électrostatique entre deux charges ponctuelles, s’écrit :
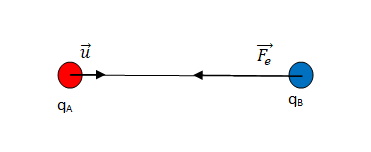
\[\Large \overrightarrow{F_e} = k.\frac{q_A.q_B}{d^2}.\overrightarrow{u} \]
Ici, qA et qB sont de signes opposés, donc l’interaction est attractive.
–Si les charges sont de mêmes signes, l’interaction électrostatique est répulsive.
–Si les charges sont de signes opposés, l’interaction électrostatique est attractive.
C’est une différence par rapport à l’interaction gravitaionnelle qui est toujours attractive.
Exemple :
Calculer la valeur de l’interaction électrostatique s’exerçant sur l’électron d’un atome d’hydrogène en mouvement autour du proton.
Données :
Charge élémentaire : \[\Large e = 1,6 \times 10^{-19} \; C\]
Rayon de l’atome d’hydrogène : \[\Large R = 53 \; pm \]
Constante électrostatique : \[\Large k = \frac{1}{4.\pi.\epsilon_0} = 9.10^9 N.m^2.C^{-2} \]
Conversion des picomètres en mètres : \[\Large 1 \; pm = 10^{-12} \; m \]
Réponse :
\[ \Large F_e = k.\frac{|e \times (-e)|}{R^2} = k.\frac{e^2}{R^2}\]
Application numérique :
\[ \Large F_e = 9.10^9.\frac{(1,6.10^{-19})^2}{(53.10^{-12})^2} = 8,2 \times 10^{-8} \; N\]
IV- Lignes de champ.
Les lignes de champ permettent de matérialiser un champ dans l’espace.
Par définition, les lignes de champ sont tangentes aux vecteurs du champ en tout point de l’espace et inversement.
Exemples de lignes de champ :
- Champ électrique créé par deux charges.
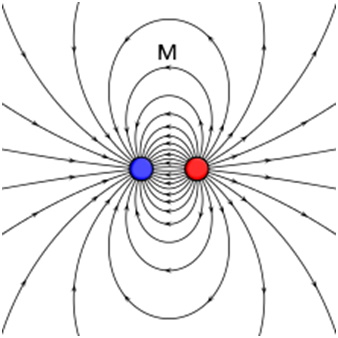
- Champ électrique entre les plaques d’un condensateurs.
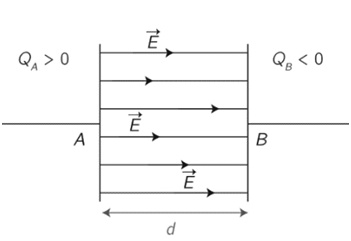
Les lignes de champ sont parallèles, donc le champ est uniforme (même direction, même sens et même valeur)
- Champ gravitationnel terrestre :
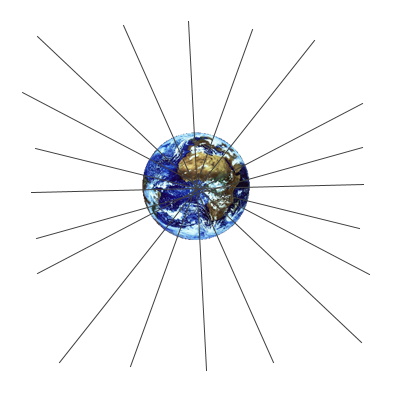
Localement, le champ gravitationnel et le champ de pesanteur sont uniformes
Interactions fondamentales et introduction à la notion de champ
https://physiquechimie.info/Interactions-fondamentales-et-notion-de-champ/