Le mouvement des systèmes mécaniques
Une chronophotographie correspond à l’enregistrement à intervalles de temps réguliers de la position d’un système. On obtient ainsi une chronophotographie. Une chronophotographie peut être obtenue à partir d’une séquence vidéo.
Grâce à un logiciel d’acquisition (Regressi, atellier scientifique, Avi-méca,… ), il est possible de pointer les positions successives d’un point de chaque image.
On obtient ainsi un enregistrement de la trajectoire du point étudié.
1. Calcul d’une vitesse à partir d’un enregistrement.
La chronophotographie ci-dessous représente l’enregistrement d’un point d’une voiture au cours du temps, roulant en ligne droite. La masse du véhicule vaut m = 700 kg. Les points ont été relevés à intervalles de temps égaux 𝜏 = Δt = 60 ms. Echelle 1/20ème.
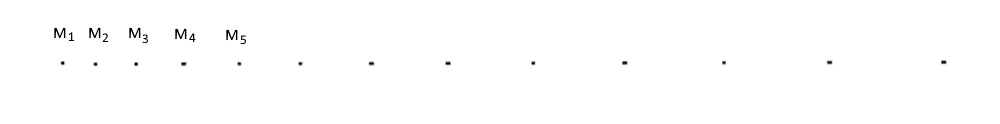
Déterminons la vitesse du véhicule en M3 et en M4, en calculant la vitesse moyenne sur un petit intervalle autour du point considéré. Plusieurs défintions de la vitesse sont possibles :
Ancienne définition :
\[\Large v_3 = \frac{M_2M_4}{2\Delta t} \]Nouvelle définition :
\[\Large v_3 = \frac{M_3M_4}{\Delta t} \]
Application numérique (2ème formule) au point M3 :
\[ M_3M_4 = 0,50 \ cm \] soit à en taille réelle :
\[ M_3M_4 = 0,50 \times 20 = 10 \ cm = 0,10 \ m \]
et
\[ \Delta t = 60 \ ms = 0,060 s\]
d’où la vitesse en M3 :
\[ v_3 = \frac{0,10}{0,060} = 1,7 \ m.s^{-1} \]
Application numérique (2ème formule) au point M4 :
\[ M_4M_5 = 0,70 \ cm \] soit en taille réelle :
\[ M_4M_5 = 0,70 \times 20 = 14 \ cm = 0,14 \ m \]
et
\[ \Delta t = 60 \ ms = 0,060 s\]
d’où la vitesse en M3 :
\[ v_4 = \frac{0,14}{0,060} = 2,3 \ m.s^{-1} \]
Pour tracer les vecteurs vitesse, il faut définir une échelle.
Par exemple :
1,0 cm pour 1,0 m.s-1, d’où la norme des vecteurs vitesse :
\[ ||\overrightarrow{v_3}|| = 1,7 \; cm \; et \; ||\overrightarrow{v_4}|| = 2,3 \; cm \]
Le vecteur vitesse doit être tangent à la trajectoire et dans le sens du mouvement.
2. Le vecteur variation de vitesse.
Le vecteur variation de vitesse est défini par :
\[ \Delta \overrightarrow{v_3} = \overrightarrow{v_4} - \overrightarrow{v_3}\]
ou sur deux intervalles de temps :
\[ \Delta \overrightarrow{v_3} = \overrightarrow{v_4} - \overrightarrow{v_2}\]
Le mouvement des systèmes mécaniques