Vision et image : l’œil et les lentilles [images et couleurs]

Quel point commun y a-t-il entre un appareil photo et un oeil ? Qu’est-ce qu’une lentille ?
Comment construire l’image d’un objet formée par une lentille convergente ? Comment calculer la position de cette image par rapport à la lentille ?
Voici les questions auxquelles nous allons répondre.

1.      Le modèle de l’œil.

On peut modéliser un œil ou un appareil photographique avec une lentille convergente et un écran, plus éventuellement un diaphragme.   Les analogies entre l’œil réel, sa modélisation et l’appareil photographique sont représentées ci-dessous. 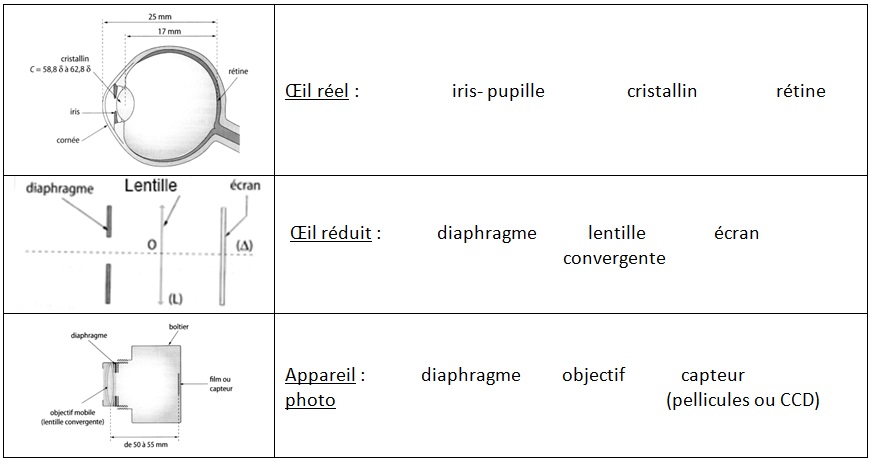    L’œil voit net à toutes les distances (ou presque). C’est le phénomène d’accommodation. Pour un appareil photo. on parle de mise au point. Lors de l’accommodation, le cristallin se déforme modifiant ainsi sa vergence, de façon à obtenir toujours une image nette sur la rétine. La mise au point d’un appareil photographique s’effectue en modifiant la distance entre l’objectif et le capteur (pellicule ou capteur CCD).

2.       Comment construire l’image d’un objet par une lentille convergente ?

2.1. Les lentilles convergentes et divergentes.

Il existe plusieurs types de lentilles 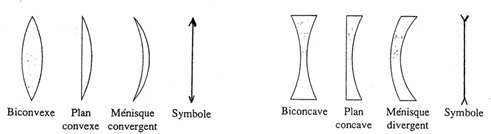Les lentilles à bords minces  sont des **lentilles convergentes ** Les lentilles à bords épais sont des lentilles divergentes.  

2.2. Les différents éléments caractéristiques d’une lentille convergente

foyer (principal) objet F, foyer (principal) image F’, centre optique O.  

2.3. La vergence et la distance focale

Par définition, la distance focale vaut \[ f’ = \overline{OF’} \] La barre au-dessus signifie qu’il s’agit d’une mesure algébrique, c’est-à-dire une longueur avec un signe. Pour une lentille convergente, la distance focale f’ est positive et est égale à OF’. La vergence notée C ou V, s’exprime en dioptries (δ) est égal à l’inverse de la distance focale en mètres (m) \[ C = \frac{1}{f’} \]   2.4. Le trajet de quelques rayons particuliers.  

• Tout rayon incident passant par le centre optique n’est pas dévié.

  

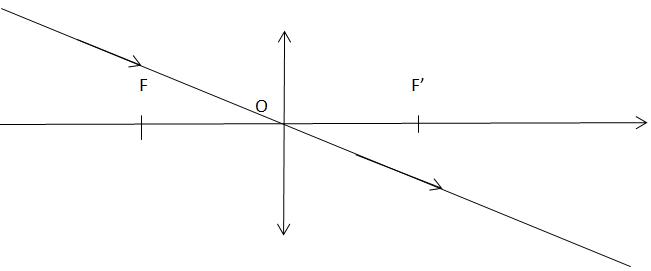
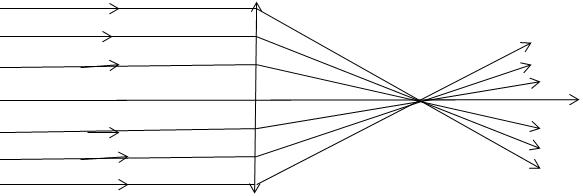
• Tout rayon incident parallèle à l’axe optique émerge en passant par le foyer image F’.

  

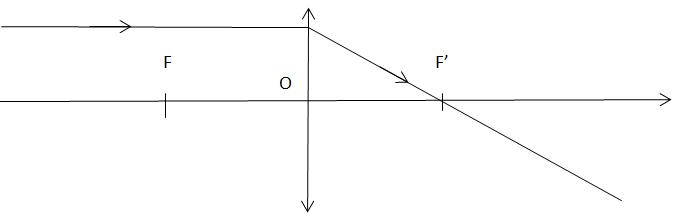
• Tout rayon incident passant par ce foyer objet F, de la lentille émerge parallèlement à l’axe optique.

   

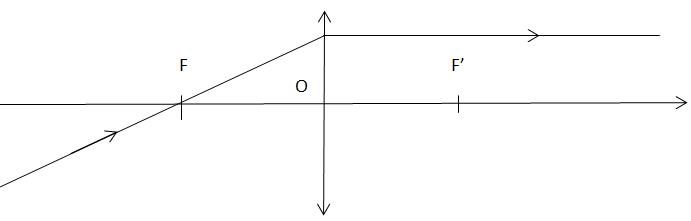
• Un faisceau de rayons passant par le foyer objet F, émerge parallèle à l’axe optique.

  

 

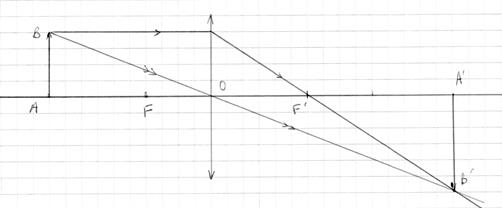
2.5. Construction de l’image d’un objet par une lentille convergente. Les points conjugués : A  tout point d’un objet correspond un point image. Donc tous les rayons issus d’un même point objet passent par le même point image.   2.5.1.        Image d’un objet situé avant le foyer objet de la lentille.

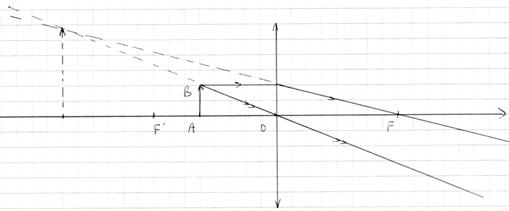2.5.2.        Image d’un objet situé entre le foyer objet et la lentille.     3.le grandissement et la relation de conjugaison de Descartes.   3.1. Le grandissement transversal gamma Par définition le grandissement vaut:   \[ \gamma =   \frac{\overline{OA’}}{\overline{OA}} \]   Si gamma > 0, l’image est droite, dans le même sens que l’objet. Si gamma <0 , l’image est renversée ou inversée par rapport à l’objet. Si la valeur absolue de gamma (nombre sans son signe) est supérieur à 1, l’image est plus grande que l’objet. Si la valeur absolue de gamma est inférieur à 1, l’image est plus petite que l’objet. 3.2. La relation de conjugaison de Descartes. Pour déterminer la position d’un point image A’ ou d’un objet objet A par rapport au centre optique O peut ce calculer par la **relation de conjugaison de DESCARTES.** \[   \frac{1}{\overline{OA’}} - \frac{1}{\overline{OA}} = \frac{1}{f’} \] Faire attention aux signes. Si le point A est avant O : \[  \overline{OA}  < 0 \] Si A’ est après O, l’ image est réelle \[  \overline{OA’}  > 0 \] Si A’ est après O, l’image est virtuelle \[   \overline{OA’} < 0 \]